Component Form of a Vector. Lets consider a position vector vecOP of a point P x y z as shown below.

Memorising Technique For A B And C D Formulae How To Memorize Things Studying Math Math Formulas
The components of the force vector can also be arranged this way forming a right triangle.
Vector component form formula. Find the component form of with initial point. The trigonometric ratios give the relation between magnitude of the vector and the components of the vector. Rectangular component of a VectorThe projections of vector Aalong the x y and zdirections are Ax Ay and Azrespectively.
Two vectors are equal when their corresponding scalar components are equal. In three dimensions as in two vectors are commonly expressed in component form or in terms of the standard unit vectors Properties of vectors in space are a natural extension of the properties for vectors in a plane. 17 - Calculating Vector Components in Physics Part 1 Component form of a Vector - YouTube.
V x V cos θ. Force vector component mathematics If we know the size of the two dimensional force vector the black one in the above diagram and the angle it makes with the x-axis then we can use right triangle trigonometry to find the values for the components. Therefore the formula to find the components of any given vector becomes.
Projection of uon v. Cos θ Adjacent Side Hypotenuse v x v. As we mentioned earlier the two vector components of a vector v are vx and vy.
Given two point v. Learn how to write a vector in component form given two points and also how to determine the magnitude of a vector given in component form. A vector functions of a single variable in R2 R 2 and R3 R 3 have the form r t f tgt r t f tgtht r t f t g t r t f t g t h t.
Where V is the magnitude of vector V and can be found using Pythagoras theorem. Magnitude of a Vector. First find the sine of 22 then multiply by 7.
When there was a free-body diagram depicting the forces acting upon an object. Cartesian components of vectors mc-TY-cartesian1-2009-1 Any vector may be expressed in Cartesian components by using unit vectors in the directions of the coordinate axes. Vectors can be easily represented using the co-ordinate system in three dimensions.
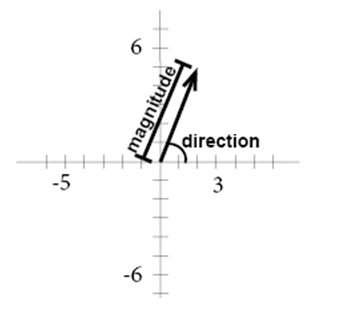
A vector is a quantity that has both magnitude and direction. For v x. Let and be vectors and let be a scalar.
1 1 3 and x. Thus vin component form v 1 v 2. B z - A z Library.
V y Vsin θ. Respectively where f t f t gt g t and ht h t are called the component functions. The vector in the component form is v 4 5.
Vecfracv2r vecfracMGr2 The centripetal force is directed. To find the vertical component set up an equation involving sine since the side in the implied triangle that represents the vertical component is opposite the 22-degree angle. Component form of a vector with initial point and terminal point.
A vector in standard position can be represented by the coordinates of its terminal point. Fracv2r fracMGr2 Im trying to understand this as a net of forces in vector form assuming a unit mass in these formulas. Typically a physics problem gives you an angle and a magnitude to define a vector.
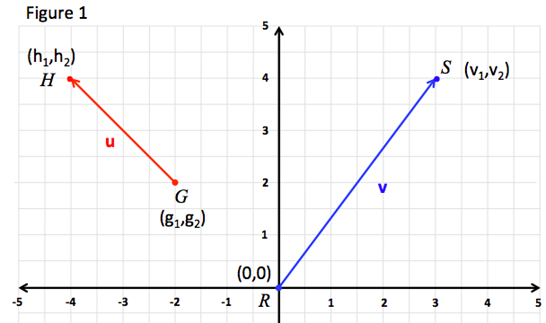
VecAB sqrtx_1 x_02 y_1 y_02 Now if the starting point is at x y and the endpoint is at the origin then the magnitude of a vector formula becomes. Following are the formulas for the calculation of the magnitudes of the two vector components. 1 Component form 1 1 3 3 x.
You have to find. Therefore by distance formula the magnitude of vector vecAB can be written as. AB B x - A x.
The projection of uon vdenoted projvuis the vector obtained by multiplying a unit vector. V v x 2 v y 2 Orthogonal vectors. For example in the vector 4 1 the x-axis horizontal component is 4 and the y-axis vertical component is 1.
As shown in the figure Let P 1 be the foot of the perpendicular from point P on the plane XOY. To completely solve the vector v in terms of magnitude and direction we would need to calculate these components first. Before getting into the representation of vectors let us understand what.
In the first couple of units all vectors that we discussed were simply directed up down left or right. Displacement velocity acceleration and force are the vector quantities that we have discussed thus far in the Physics Classroom Tutorial. B y - A y.
In this unit we describe these unit vectors in two dimensions and in three dimensions and show how they can be used in calculations. In physics when you break a vector into its parts those parts are called its components. Finding Magnitude Of The Vector Components.
2 1 3 0 6 Subtract. The component form of vector AB with AA x A y A z and BB x B y B z can be found using the following formula. Express a Vector in Component Form.
Vector v in Figure 1 has an initial point at the origin 00 and is said to be in standard position. We are familiar with the equation for calculating the velocity of an object in orbit given the central mass or the mass given the orbital velocity. Direction CosinesCosa CosbCosg Unit vector along a vectorTheunit vector uAalong the vector Aisobtained from.
A 1 3 and terminal point. Vectors are often represented in component form. Resolving vectors into their scalar components ie finding their scalar components and expressing them analytically in vector component form given by Equation 219 allows us to use vector algebra to find sums or differences of many vectors analytically ie without using graphical methods.
In fact it is easy to calculate thatcompvu u exactly whenuis in the direction of vandcompvu u exactly whenuis in the direction opposite that of v. Vector or Cross Product of Two Vectors.

Jasmine On Instagram I M Quite Behind On Answering Dms I Ve Been Really Busy With Schoolwork And E School Organization Notes Notes Inspiration College Notes

Matrix Element Row Column Order Of Matrix Determinant Types Of Matrices Ad Joint Transpose Of Matrix Cbse Math 12th Product Of Matrix Math Multiplication

Express A Vector In Component Form Precalculus

How To Find Shortest Distance Between Two Lines Simplifying Mathematics In Simple Way Geometry Lesson Plans Coordinate Plane Graphing Classroom Math Stations

Vectors Geometry Transformations Mathplanet
Vector Forms Review Article Vectors Khan Academy

Checklist For Solving Statics Problems Engineering Notes Engineering Mechanics Statics Learning Math

Directional Derivative And Gradient Vector With Example In Python Code Coding Calculus Derivative
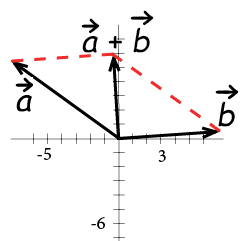
Vectors Geometry Transformations Mathplanet

What Is Symmetric And Skew Symmetric Matrix How To Know Whether Any Given Matrix Is Symmetric Or Skew Symmetric And How To Co Matrix Mathematics Mathematician

Hand Drawn Geometry Formulas Science Knowledge Education Ad Ad Geometry Drawn Hand Formulas Geometry Formulas How To Draw Hands Math Wallpaper

Damped Sine Wave Formula Grasshopper Sine Wave Waves Grasshopper

What Are Vectors Easily Explained With 17 Examples Math Methods Math Courses Learning Math

Components Of A Vector Unit Vector Length And Sum Videos Examples