What is the Magnitude of VectorE. A ruler and protractor are not needed for this exercise.
How To Find The Resultant Of Two Vectors Youtube
The trigonometric ratios give the relation between magnitude of the vector and the components of the vector.
Rewrite vector in component form. From the point P two perpendicular PN and PM are dropped on. To find the vector in component form given the initial and terminal points simply subtract the. Through the point O two mutually perpendicular axis X and Y are drawn.
Write VectorE In component Form. In this case the vector is in standard form therefore the components of the vector are the same as the components of the terminal point. Calculate directions and magnitudes of vectors.
Each part of a two-dimensional vector is known as a component. Eqv_y vsin Theta eq Step 3. What is the direction of Vector E.
A tns file is provided to students for this. Write x y and z in component form as Then rewrite the vector as a linear combination of the standard unit vectors. This is known as component form and is expressed as r ai bj.
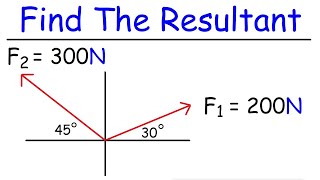
Calculate the magnitude in centimeters and direction in standard form of the resultant vector for each diagram using the method of components. Then rewrite the vector as a linear combination of the standard unit vectors. Find the horizontal displacement eqv_x x_2 - x_1 eq where eqx_2 eq is the eqx- eqcoordinate of the terminal point.
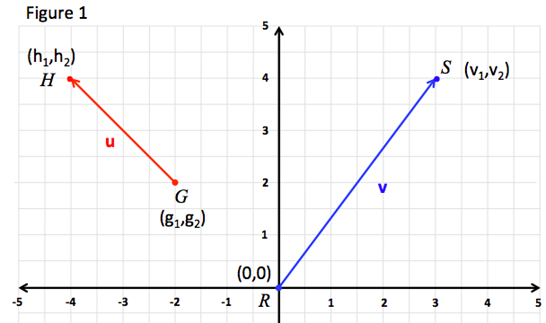
Consider one box as one unit in terms of magnitude. Subtract the x-component of the terminal point from the x-component of the initial point for your x-component of the vector. In the Cartesian coordinate system any vector vecp can be represented in terms of its unit vectors.
This video demonstrates by example how to convert a vector in polar form to component for and how to convert a vector in component form to polar form. There are a number of ways that 2D vectors can be represented. Vectors are comprised of two components.
Rectangular components of a vector. Rewrite vector in component form STEM_GP12V-Ia-10-11 b. Do the same for the y-components.
Find the component form of the vector with. 5 9 Component form 5. The vector is normally visualized in a graph.
Let 5 2 -3 - 5 and 2 3. Express A Vector In Component Form. J a b a.
Calculate the components of the vector. 8x 2y 5 z 628721 Write x y and z in component form as Then rewrite the vector as a linear combination of the standard unit vectors. The components of a vector depict the influence of that vector in a.
The figure illustrates a vector overrightarrowA represented by overrightarrowOP. Write the vector in component form. First find the component form of.
If the components of a given vector are perpendicular to each other they are called as Rectangular components. You then need just to rewrite the vector in its component form using the rise and run components. The vector in the component form is v 4 5.
X 4y í z. Rewrite the vectors in their component forms. The ordered pair that describes the changes is x2- x1 y2- y1 in our example 2-0 5-0 or 25.
The component form of a vector is the ordered pair that describes the changes in the x- and y-values. Find the x-component of vector v. Identify the components of vectors.
Component Form of Vector. Find the y-component of vector v. Convert a vector between standard form and component form and back.
COMPONENTS OF VECTOR Learning Competency a. 100 5 ratings Transcribed image text. Eqv_x vcos Theta eq Step 2.
In the graph above x10 y10 and x22 y25. This is the best answer based on feedback and ratings. In the graph above x 1 0 y 1 0 and x 2 2 y 2 5.
D í3 15 Eí3 15 628721 First find the component form of. Show transcribed image text Best Answer. Appreciate the importance of using vectors.
Write the new vector in component form. Vectors can be written as components or as a magnitude and direction. Rewrite vectors in their component forms.
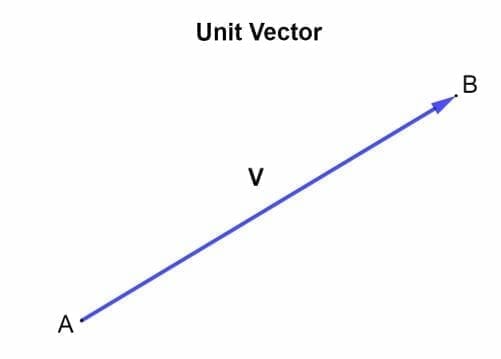
V A V B 0 0 V e c t o r V x w it h d ir e c ti o n V y w it h d ir e c ti o n V A 1 2 V B 3 4 Looking at the figure on the left its component Vx covers 4 units in the graph going to a rightward or Eastward direction while its component Vy covers 5 units going to an upward or Northward direction. In some applications involving vectors it is helpful for us to be able to break a vector down into its components. Writing a Vector in Component Form Given its Endpoints.
Cos θ Adjacent Side Hypotenuse v x v. That is it can be thought of as having two parts. Any vector directed in two dimensions can be thought of as having an influence in two different directions.
The rules of trigonometry can be used to convert between the different representations. The unit vectors in direction of xy and z-axes are given by hati hatj and hatk respectively. Example Question 1.
For the working example the new vector will be. Use the 1 cm grid lines towards this end. The horizontal component is the direction and the vertical component is the direction.
Then rewrite the vector as a linear combination of the standard unit vectors. Calculate directions and magnitudes of vectors STEM_GP12V-Ia-11 Learning Objectives a. Knowing the slope is almost the final step.
Then rewrite the vector as a linear combination of the standard unit vectors. A vector that is directed upward and rightward can be thought of as having two parts - an upward part and a rightward part. So we have two examples here where were given the magnitude of a vector and its direction and the direction is by giving us an angle that it forms with the positive x-axis what we need to do is go from having this magnitude in this angle this direction to figuring out what the x and y components of this vector actually are so like always pause this video and see if you can if you can work through this on.
The position of vector vecp can be represented in space with respect to the origin of the. A vector between A and B is written as overrightarrowAB The vectors standard position has its starting point in origin. One of these representations involves expressing a vector r in terms of unit vectors i and j.
The component form of a vector is the ordered pair that describes the changes in the x- and y-values. Vectors are used to represent quantities that have both magnitude and direction.

Vectors In A Plane Pre Calculus Section Ppt Download
6 04 Writing Vectors In Trigonometric Form

Vectors Sections 6 6 Objectives Rewrite A Vector
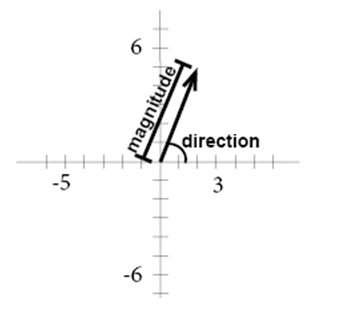
Vectors Geometry Transformations Mathplanet
Unit Vectors And Components Ck 12 Foundation
6 04 Writing Vectors In Trigonometric Form
Vector Forms Review Article Vectors Khan Academy

Express A Vector In Component Form Precalculus

Vectors In Rectangular Form Youtube

React Native Vector Icons Vector Icons React Native Icon

Vectors In A Plane Pre Calculus Section Ppt Download
Vec 0040 Linear Combinations Of Vectors Ximera
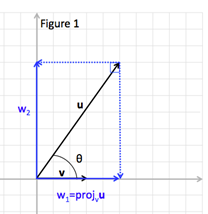
Decomposing A Vector Into Components
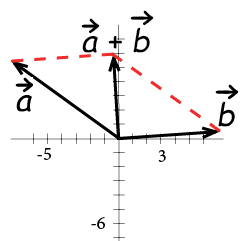
Vectors Geometry Transformations Mathplanet